Summary

Github Repo

Problem Statement: Automate the schedule creation process for a snack shop while accounting for current metrics used in manual schedule creation.

Project Details: This is a project I did of my own volition during winter break of my sophomore year. It was made using python and the openpyxl package. It is only partially completed and does not have the final touches I wish it did. Although the code is not the prettiest and is missing some features I am still proud of the underlying algorithm which this post will focus heavily on. I took user availability and working time preferences from an excel sheet which was read by the program and then an optimal schedule was created and formatted into another excel sheet for printing and distribution.

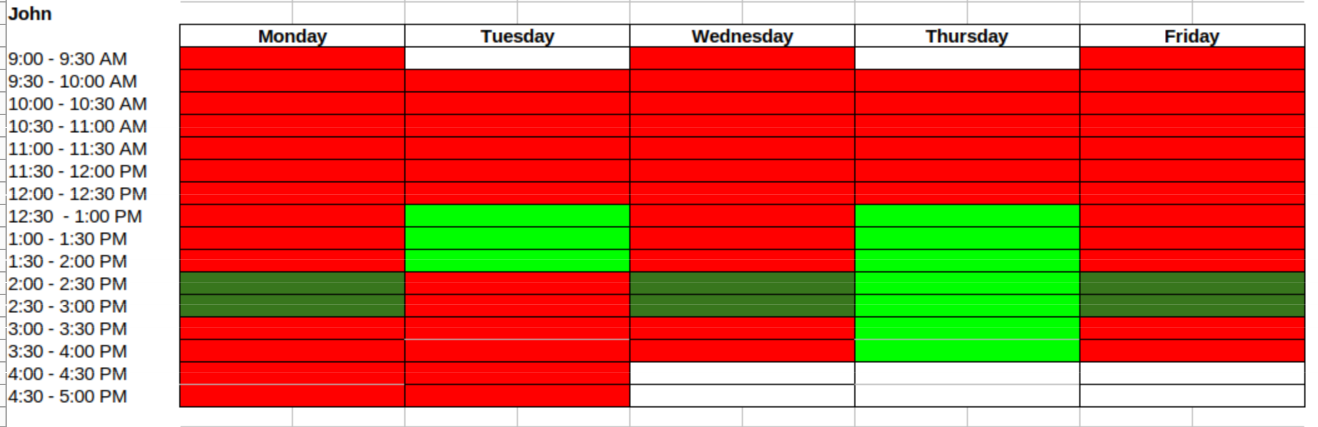
Project Background: The schedule that this program creates is for a student org snack shop. There are 16 officers that each have 3 hours a week. The shop is open 8 hours a day 5 days a week. The image below shows an example of how one would fill out their availability. The red indicates unavailable, the white indicates available, the light green indicates preferred, and the dark green indicates ideal. The cover image in this post is the final result of the program.

Example Availability

Functional Overview

Defining an Optimal Schedule: In order to create an optimal schedule I first had to look at how to quantify what metrics I was looking at. The steps/rules below are how a schedule is ranked once it has been created. The rules are followed in priority as listed below so that more important metrics are considered first.

1. No three hours in one day for one person. (Always want to avoid this situation)
2. Least available but not preferred hours used. (Not hours that people want)
3. Fewest joint hours per person. (Equally distribute shared hours)
4. Least 2 hours in 1 day. (Space each persons hours throughout the week)
5. Least 2 hours in a row. (If possible stop minimize amount of 2 hours in a row for someone)
6. Least amount of light green. (Focus on ideal hours)
7. Least middle hour of 3 hour blocks. (When a person has 3 hours of straight availability try and pick the first or last hour)

Class Based Structure: This program utilizes object oriented program and python classes in order to effectively accomplish the goal. I created classes for both the officer and the schedule. This allowed me to store availability for each officer and the schedule created as well as it’s metrics within the corresponding class. I was also able to create functions for each class such as ones for getting an officer’s availability and for getting metrics from a schedule.

Core Algorithm: The main algorithm behind this program uses a tree based structure with a combination of breadth and depth first searches. The root of the tree is an empty schedule and a child is created for each officer available within the first hour of the first day. This process is repeated for each hour under each child and added to the queue. Children are added to the queue with those representing an addition of an Ideal or Preferred hour first.

Once the queue reaches a size of 10,000 the search is switched to a depth first search until it returns below 10,000. Due to the order of placement in the queue when it is treated as a stack schedules with more Ideal hours tend to appear first. When a complete possible schedule is found it is added to the list of solutions and it’s metrics are recorded. From then on new schedules are only added if they are equal in metrics rankings. If a better schedule is found the list is reset as well as the comparison metrics.

If the program checked every possible schedule combination it would take days or weeks to run. In order to optimize the run time each branch has it’s metrics tracked as new children are created. If the branch gets to a point where it will never have better rankings than the current best solution then the branch is removed and no further search will be done on it. This drastically decreases the amount of nodes searched and in turn decreases computing time.

During my testing the input data I used tended to search 340 million nodes and locate 1.6 million solutions in ~40 minutes of runtime before determining that the optimal solution had been found.

If I Did It Again: This project was great for practicing programming and using skills I had learned about data structures and algorithms. Although I am proud of the results there are many things I would change looking back on the project. Below is a list of those changes.

1. Use a different language for faster run times and using multithreading.
2. Generalize the inputs to improve the capabilities for different amounts of people and open hours.
3. Store the current status of the program occasionally in case the computer shuts down.
4. Change the data structures to use matrices containing integers instead of objects for quicker operations using matrix math.